Saturday 8 December 2012
Thursday 6 December 2012
Thursday 22 November 2012
Wednesday 31 October 2012
Thursday 25 October 2012
Sunday 7 October 2012
Thursday 27 September 2012
Pantun Teka-Teki Berkaitan Tambah
Soalan:
Cantik sungguh kereta Kenari, 13 + 4 = ?
Dibeli oleh seorang nyonya,
Kalau anda bijak bistari,
Tiga belas tambah empat apa jawapannya ?
Jawab jangan tak jawab....agak-agak ada tak yang nak jawab pantun ini ? Saya ada satu lagi pantun. Dengar ye...
Makan tempe dengan tauhu, 24 + 9 = ?
Ubi kayu cicah kelapa,
Saya di sini ingin nak tahu,
Dua puluh empat tambah sembilan sama dengan berapa ?
Cukuplah 2 pantun dulu. Nanti lain kali saya akan masukkan lagi. Aktiviti ini kita boleh jalankan semasa aktiviti kumpulan dijalankan. Kira gabungjalin dengan mata pelajaran Bahasa Melayu la ni. Baiklah kawan-kawan. Semoga berjumpa lagi di lain masa. Selamat mencuba.
Monday 24 September 2012
Friday 21 September 2012
Thursday 20 September 2012
Pembahasan Soal Ujian: TEKA-TEKI : Matematika Logika
Pembahasan Soal Ujian: TEKA-TEKI : Matematika Logika: Teka-teki berikut bukan sembarang teka-teki. Teka-teki ini juga akan mengetes SEBERAPA CERDASNYA ANDA DALAM MENGGUNAKAN LOGIKA BERFIKIR ...
Wednesday 19 September 2012
What is Mathematics?
From Wikipedia, the free encyclopedia
Maths" and "Math" redirect here.
For other uses see Mathematics
(disambiguation) and Math (disambiguation).
Maths" and "Math" redirect here.
For other uses see Mathematics
(disambiguation) and Math (disambiguation).
Mathematics (from Greek μάθημα máthēma "knowledge, study, learning") is the study of quantity, space, structure, and change.[2][3]Mathematicians seek out patterns[4][5] and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures bymathematical proofs, which are arguments sufficient to convince other mathematicians of their validity. The research required to solve mathematical problems can take years or even centuries of sustained inquiry. However, mathematical proofs are less formal and painstaking than proofs in mathematical logic. Since the pioneering work of Giuseppe Peano, David Hilbert, and others on axiomatic systems in the late 19th century, it has become customary to view mathematical research as establishing truth by rigorous deduction from appropriately chosenaxioms and definitions. When those mathematical structures are good models of real phenomena, then mathematical reasoning often provides insight or predictions.
hrough the use of abstraction and logical reasoning, mathematics developed from counting, calculation, measurement, and the systematic study of the shapes and motions of physical objects. Practical mathematics has been a human activity for as far back as written records exist.Rigorous arguments first appeared in Greek mathematics, most notably in Euclid's Elements. Mathematics continued to develop, for example in China in 300 BC, in India in AD 100[citation needed], and in the Muslim world in AD 800, until the Renaissance, when mathematical innovations interacting with new scientific discoveries led to a rapid increase in the rate of mathematical discovery that continues to the present day.[6]
The mathematician Benjamin Peirce called mathematics "the science that draws necessary conclusions".[7] David Hilbert said of mathematics: "We are not speaking here of arbitrariness in any sense. Mathematics is not like a game whose tasks are determined by arbitrarily stipulated rules. Rather, it is a conceptual system possessing internal necessity that can only be so and by no means otherwise."[8] Albert Einstein stated that "as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality".[9]
Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered.[10]
Etymology
The word "mathematics" comes from the Greek μάθημα (máthēma), which means in ancient Greek what one learns, what one gets to know, hence also study and science, and in modern Greek just lesson.
The word máthēma comes from μανθάνω (manthano) in ancient Greek and from μαθαίνω (mathaino) in modern Greek, both of which mean to learn.
The word "mathematics" in Greek came to have the narrower and more technical meaning "mathematical study", even in Classical times.[11] Its adjective is μαθηματικός (mathēmatikós), meaning related to learning or studious, which likewise further came to mean mathematical. In particular, μαθηματικὴ τέχνη (mathēmatikḗ tékhnē), Latin: ars mathematica, meant the mathematical art. In Latin, and in English until around 1700, the term "mathematics" more commonly meant "astrology" (or sometimes "astronomy") rather than "mathematics"; the meaning gradually changed to its present one from about 1500 to 1800. This has resulted in several mistranslations: a particularly notorious one is Saint Augustine's warning that Christians should beware of "mathematici" meaning astrologers, which is sometimes mistranslated as a condemnation of mathematicians.
The apparent plural form in English, like the French plural form les mathématiques (and the less commonly used singular derivative la mathématique), goes back to the Latin neuter pluralmathematica (Cicero), based on the Greek plural τα μαθηματικά (ta mathēmatiká), used by Aristotle, and meaning roughly "all things mathematical"; although it is plausible that English borrowed only the adjective mathematic(al) and formed the noun mathematics anew, after the pattern of physics and metaphysics, which were inherited from the Greek.[12] In English, the noun mathematics takes singular verb forms. It is often shortened to maths or, in English-speaking North America, math.
History
Main article: History of mathematics

Greek mathematicianPythagoras (c.570-c.495 BC), commonly credited with discovering the Pythagorean theorem.
The evolution of mathematics might be seen as an ever-increasing series of abstractions, or alternatively an expansion of subject matter. The first abstraction, which is shared by many animals,[13] was probably that of numbers: the realization that a collection of two apples and a collection of two oranges (for example) have something in common, namely quantity of their members.
In addition to recognizing how to count physical objects, prehistoric peoples also recognized how to count abstract quantities, like time – days,seasons, years.[14] Elementary arithmetic (addition, subtraction, multiplication and division) naturally followed.
Since numeracy pre-dated writing, further steps were needed for recording numbers such as tallies or the knotted strings called quipu used by the Incato store numerical data.[citation needed] Numeral systems have been many and diverse, with the first known written numerals created by Egyptians inMiddle Kingdom texts such as the Rhind Mathematical Papyrus.[citation needed]
The earliest uses of mathematics were in trading, land measurement, painting and weaving patterns and the recording of time. More complex mathematics did not appear until around 3000 BC, when the Babyloniansand Egyptians began using arithmetic, algebra and geometry for taxation and other financial calculations, for building and construction, and for astronomy.[15] The systematic study of mathematics in its own right began with the Ancient Greeks between 600 and 300 BC.[16]
Mathematics has since been greatly extended, and there has been a fruitful interaction between mathematics and science, to the benefit of both. Mathematical discoveries continue to be made today. According to Mikhail B. Sevryuk, in the January 2006 issue of the Bulletin of the American Mathematical Society, "The number of papers and books included in the Mathematical Reviews database since 1940 (the first year of operation of MR) is now more than 1.9 million, and more than 75 thousand items are added to the database each year. The overwhelming majority of works in this ocean contain new mathematical theorems and their proofs."[17]
Inspiration, pure and applied mathematics, and aesthetics
Main article: Mathematical beauty

Sir Isaac Newton (1643-1727), aninventor of infinitesimal calculus.
Mathematics arises from many different kinds of problems. At first these were found in commerce,land measurement, architecture and later astronomy; nowadays, all sciences suggest problems studied by mathematicians, and many problems arise within mathematics itself. For example, the physicist Richard Feynman invented the path integral formulation of quantum mechanics using a combination of mathematical reasoning and physical insight, and today's string theory, a still-developing scientific theory which attempts to unify the four fundamental forces of nature, continues to inspire new mathematics.[18] Some mathematics is only relevant in the area that inspired it, and is applied to solve further problems in that area. But often mathematics inspired by one area proves useful in many areas, and joins the general stock of mathematical concepts. A distinction is often made between pure mathematics and applied mathematics. However pure mathematics topics often turn out to have applications, e.g. number theory in cryptography. This remarkable fact that even the "purest" mathematics often turns out to have practical applications is what Eugene Wigner has called "the unreasonable effectiveness of mathematics".[19] As in most areas of study, the explosion of knowledge in the scientific age has led to specialization: there are now hundreds of specialized areas in mathematics and the latest Mathematics Subject Classification runs to 46 pages.[20] Several areas of applied mathematics have merged with related traditions outside of mathematics and become disciplines in their own right, including statistics,operations research, and computer science.
For those who are mathematically inclined, there is often a definite aesthetic aspect to much of mathematics. Many mathematicians talk about the elegance of mathematics, its intrinsic aesthetics and inner beauty. Simplicity and generality are valued. There is beauty in a simple and elegant proof, such as Euclid's proof that there are infinitely many prime numbers, and in an elegant numerical method that speeds calculation, such as the fast Fourier transform. G. H. Hardy in A Mathematician's Apology expressed the belief that these aesthetic considerations are, in themselves, sufficient to justify the study of pure mathematics. He identified criteria such as significance, unexpectedness, inevitability, and economy as factors that contribute to a mathematical aesthetic.[21] Mathematicians often strive to find proofs that are particularly elegant, proofs from "The Book" of God according to Paul Erdős.[22][23] The popularity of recreational mathematics is another sign of the pleasure many find in solving mathematical questions.
Notation, language, and rigor
Main article: Mathematical notation

Leonhard Euler, who created and popularized much of the mathematical notation used today
Most of the mathematical notation in use today was not invented until the 16th century.[24] Before that, mathematics was written out in words, a painstaking process that limited mathematical discovery.[25] Euler (1707–1783) was responsible for many of the notations in use today. Modern notation makes mathematics much easier for the professional, but beginners often find it daunting. It is extremely compressed: a few symbols contain a great deal of information. Like musical notation, modern mathematical notation has a strict syntax (which to a limited extent varies from author to author and from discipline to discipline) and encodes information that would be difficult to write in any other way.
Mathematical language can be difficult to understand for beginners. Words such as or and only have more precise meanings than in everyday speech. Moreover, words such as open and field have been given specialized mathematical meanings. Technical terms such as homeomorphism and integrablehave precise meanings in mathematics. Additionally, shorthand phrases such as "iff" for "if and only if" belong to mathematical jargon. There is a reason for special notation and technical vocabulary: mathematics requires more precision than everyday speech. Mathematicians refer to this precision of language and logic as "rigor".
Mathematical proof is fundamentally a matter of rigor. Mathematicians want their theorems to follow from axioms by means of systematic reasoning. This is to avoid mistaken "theorems", based on fallible intuitions, of which many instances have occurred in the history of the subject.[26] The level of rigor expected in mathematics has varied over time: the Greeks expected detailed arguments, but at the time of Isaac Newton the methods employed were less rigorous. Problems inherent in the definitions used by Newton would lead to a resurgence of careful analysis and formal proof in the 19th century. Misunderstanding the rigor is a cause for some of the common misconceptions of mathematics. Today, mathematicians continue to argue among themselves about computer-assisted proofs. Since large computations are hard to verify, such proofs may not be sufficiently rigorous.[27]
Axioms in traditional thought were "self-evident truths", but that conception is problematic. At a formal level, an axiom is just a string of symbols, which has an intrinsic meaning only in the context of all derivable formulas of an axiomatic system. It was the goal of Hilbert's program to put all of mathematics on a firm axiomatic basis, but according to Gödel's incompleteness theorem every (sufficiently powerful) axiomatic system has undecidable formulas; and so a final axiomatization of mathematics is impossible. Nonetheless mathematics is often imagined to be (as far as its formal content) nothing but set theory in some axiomatization, in the sense that every mathematical statement or proof could be cast into formulas within set theory.[28]
Fields of mathematics
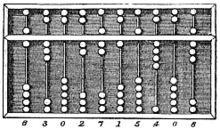
An abacus, a simple calculating tool used since ancient times.
See also: Areas of mathematics
Mathematics can, broadly speaking, be subdivided into the study of quantity, structure, space, and change (i.e. arithmetic, algebra, geometry, and analysis). In addition to these main concerns, there are also subdivisions dedicated to exploring links from the heart of mathematics to other fields: to logic, to set theory (foundations), to the empirical mathematics of the various sciences (applied mathematics), and more recently to the rigorous study of uncertainty.
Foundations and philosophy
In order to clarify the foundations of mathematics, the fields of mathematical logic and set theory were developed. Mathematical logic includes the mathematical study of logic and the applications of formal logic to other areas of mathematics; set theory is the branch of mathematics that studies sets or collections of objects. Category theory, which deals in an abstract way with mathematical structures and relationships between them, is still in development. The phrase "crisis of foundations" describes the search for a rigorous foundation for mathematics that took place from approximately 1900 to 1930.[29] Some disagreement about the foundations of mathematics continues to the present day. The crisis of foundations was stimulated by a number of controversies at the time, including the controversy over Cantor's set theory and the Brouwer-Hilbert controversy.
Mathematical logic is concerned with setting mathematics within a rigorous axiomatic framework, and studying the implications of such a framework. As such, it is home to Gödel's incompleteness theorems which (informally) imply that any formal system that contains basic arithmetic, if sound (meaning that all theorems that can be proven are true), is necessarilyincomplete (meaning that there are true theorems which cannot be proved in that system). Whatever finite collection of number-theoretical axioms is taken as a foundation, Gödel showed how to construct a formal statement that is a true number-theoretical fact, but which does not follow from those axioms. Therefore no formal system is a complete axiomatization of full number theory. Modern logic is divided into recursion theory, model theory, and proof theory, and is closely linked to theoretical computer science[citation needed], as well as to Category Theory.
Theoretical computer science includes computability theory, computational complexity theory, and information theory. Computability theory examines the limitations of various theoretical models of the computer, including the most well known model – the Turing machine. Complexity theory is the study of tractability by computer; some problems, although theoretically solvable by computer, are so expensive in terms of time or space that solving them is likely to remain practically unfeasible, even with rapid advance of computer hardware. A famous problem is the "P=NP?" problem, one of the Millennium Prize Problems.[30] Finally, information theory is concerned with the amount of data that can be stored on a given medium, and hence deals with concepts such as compression and entropy.
Pure mathematics
Quantity
The study of quantity starts with numbers, first the familiar natural numbers and integers ("whole numbers") and arithmetical operations on them, which are characterized in arithmetic. The deeper properties of integers are studied in number theory, from which come such popular results as Fermat's Last Theorem. The twin prime conjecture and Goldbach's conjectureare two unsolved problems in number theory.
As the number system is further developed, the integers are recognized as a subset of the rational numbers ("fractions"). These, in turn, are contained within the real numbers, which are used to represent continuous quantities. Real numbers are generalized to complex numbers. These are the first steps of a hierarchy of numbers that goes on to include quarternions andoctonions. Consideration of the natural numbers also leads to the transfinite numbers, which formalize the concept of "infinity". Another area of study is size, which leads to the cardinal numbers and then to another conception of infinity: the aleph numbers, which allow meaningful comparison of the size of infinitely large sets.
Structure
Space
Change
Understanding and describing change is a common theme in the natural sciences, and calculus was developed as a powerful tool to investigate it. Functions arise here, as a central concept describing a changing quantity. The rigorous study of real numbers and functions of a real variable is known as real analysis, with complex analysis the equivalent field for thecomplex numbers. Functional analysis focuses attention on (typically infinite-dimensional) spaces of functions. One of many applications of functional analysis is quantum mechanics. Many problems lead naturally to relationships between a quantity and its rate of change, and these are studied as differential equations. Many phenomena in nature can be described bydynamical systems; chaos theory makes precise the ways in which many of these systems exhibit unpredictable yet still deterministic behavior.
Applied mathematics
Applied mathematics concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge. The term "applied mathematics" also describes the professional specialty in which mathematicians work on practical problems; as a profession focused on practical problems, applied mathematics focuses on the formulation, study, and use of mathematical models in science, engineering, and other areas of mathematical practice.
In the past, practical applications have motivated the development of mathematical theories, which then became the subject of study in pure mathematics, where mathematics is developed primarily for its own sake. Thus, the activity of applied mathematics is vitally connected with research in pure mathematics.
Statistics and other decision sciences
Applied mathematics has significant overlap with the discipline of statistics, whose theory is formulated mathematically, especially with probability theory. Statisticians (working as part of a research project) "create data that makes sense" with random sampling and with randomized experiments;[31] the design of a statistical sample or experiment specifies the analysis of the data (before the data be available). When reconsidering data from experiments and samples or when analyzing data from observational studies, statisticians "make sense of the data" using the art of modelling and the theory of inference – with model selection and estimation; the estimated models and consequential predictions should be tested on new data.[32]
Statistical theory studies decision problems such as minimizing the risk (expected loss) of a statistical action, such as using a procedure in, for example, parameter estimation,hypothesis testing, and selecting the best. In these traditional areas of mathematical statistics, a statistical-decision problem is formulated by minimizing an objective function, like expected loss or cost, under specific constraints: For example, a designing a survey often involves minimizing the cost of estimating a population mean with a given level of confidence.[33] Because of its use of optimization, the mathematical theory of statistics shares concerns with other decision sciences, such as operations research, control theory, andmathematical economics.[34]
Computational mathematics
Mathematics as profession
The best-known award in mathematics is the Fields Medal,[35][36] established in 1936 and now awarded every 4 years. It is often considered the equivalent of science's Nobel Prizes. TheWolf Prize in Mathematics, instituted in 1978, recognizes lifetime achievement, and another major international award, the Abel Prize, was introduced in 2003. The Chern Medal was introduced in 2010 to recognize lifetime achievement. These are awarded for a particular body of work, which may be innovation, or resolution of an outstanding problem in an established field.
A famous list of 23 open problems, called "Hilbert's problems", was compiled in 1900 by German mathematician David Hilbert. This list achieved great celebrity among mathematicians, and at least nine of the problems have now been solved. A new list of seven important problems, titled the "Millennium Prize Problems", was published in 2000. Solution of each of these problems carries a $1 million reward, and only one (the Riemann hypothesis) is duplicated in Hilbert's problems.
Mathematics as science

Carl Friedrich Gauss, known as the "prince of mathematicians".[37]
Carl Friedrich Gauss referred to mathematics as "the Queen of the Sciences".[38] In the original Latin Regina Scientiarum, as well as in German Königin der Wissenschaften, the word corresponding to science means a "field of knowledge", and this was the original meaning of "science" in English, also. Of course, mathematics is in this sense a field of knowledge. The specialization restricting the meaning of "science" to natural science follows the rise of Baconian science, which contrasted "natural science" to scholasticism, the Aristotelean method of inquiring from first principles. Of course, the role of empirical experimentation and observation is negligible in mathematics, compared to natural sciences such as psychology, biology, or physics.Albert Einstein stated that "as far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality."[9]
Many philosophers believe that mathematics is not experimentally falsifiable, and thus not a science according to the definition of Karl Popper.[39]However, in the 1930s Gödel's incompleteness theorems convinced many mathematicians[who?] that mathematics cannot be reduced to logic alone, and Karl Popper concluded that "most mathematical theories are, like those of physics and biology, hypothetico-deductive: pure mathematics therefore turns out to be much closer to the natural sciences whose hypotheses are conjectures, than it seemed even recently."[40] Other thinkers, notably Imre Lakatos, have applied a version of falsificationism to mathematics itself.
An alternative view is that certain scientific fields (such as theoretical physics) are mathematics with axioms that are intended to correspond to reality. In fact, the theoretical physicist, J. M. Ziman, proposed that science is public knowledge and thus includes mathematics.[41] In any case, mathematics shares much in common with many fields in the physical sciences, notably the exploration of the logical consequences of assumptions. Intuition andexperimentation also play a role in the formulation of conjectures in both mathematics and the (other) sciences. Experimental mathematics continues to grow in importance within mathematics, and computation and simulation are playing an increasing role in both the sciences and mathematics, weakening the objection that mathematics does not use the scientific method.[citation needed]
The opinions of mathematicians on this matter are varied. Many mathematicians[who?] feel that to call their area a science is to downplay the importance of its aesthetic side, and its history in the traditional seven liberal arts; others[who?] feel that to ignore its connection to the sciences is to turn a blind eye to the fact that the interface between mathematics and its applications in science and engineering has driven much development in mathematics. One way this difference of viewpoint plays out is in the philosophical debate as to whether mathematics is created (as in art) or discovered (as in science). It is common to see universities divided into sections that include a division of Science and Mathematics, indicating that the fields are seen as being allied but that they do not coincide. In practice, mathematicians are typically grouped with scientists at the gross level but separated at finer levels. This is one of many issues considered in the philosophy of mathematics.[citation needed]
Subscribe to:
Posts (Atom)